[Please watch the video attached at the end of this blog for a visual explanation of this topic]
This article is focused on the subtopic of “Simplifying Algebraic Expressions” under the main topic of “Algebra”, which happens to be a commonly questioned area in Mathematics. In fact, it is nearly impossible to find a Mathematics paper without a question on simplifying algebraic expressions.
What does it mean when we “want to simplify algebraic expressions”?
This simply means that we rewrite a given algebraic expression in simpler terms. We sort out the “messy” bits of the expression by adding, subtracting, multiplying and/or dividing, and we make the expression look neater.
That is the surface level explanation of it. The theory behind it is a bit more complex but also interesting once a person gets the hang of it. Without further ado, let’s read right on!
Using Addition and Subtraction to simplify an expression
In simplifying expressions, if we are adding or subtracting, we need to see whether the letter is the same. If it is the same letter, then you can add it together and these are known as “like terms”.
So
4b +6b = 10b
7e – 5e = 2e
This is like normal mathematics.
If the letters are not the same, for example, if the letters are x and y, then these letters are different and they are known as “unlike terms”.
Now, if we consider the subtraction of this expression: 3x^2 – x^2 since we have two values with x^2 where the powers are the same, we consider them to be like terms and the normal mathematical subtraction can be carried out.
3x^2 – x^2= 2x^2
(Although there is no number in front of x^2 in the question, we consider it to be a 1)
However in the example expression 6bc – 9ab, then once again you cannot subtract it because these are unlike terms (bc and ab are different from one another)
Always Remember!
- In order to simplify, you must only have like terms.
Simplifying by Combining the Like Terms
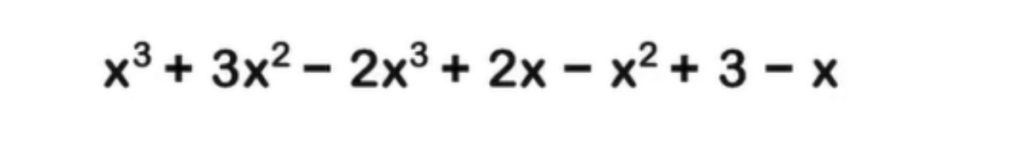
When looking at this example, we can see that it appears hard to simplify this. Therefore to make this simpler, we will group like terms together. We look at the two terms which have the power three (x^3 and -2x^3) and group them together.
When grouping, remember to take the sign in front of the number (either positive + or negative -) as well. In this case, we must take the negative ( – ) sign in front of 2x^3.
Using the same method, we can then group the power two values ( + 3x^2 and – x^2) and the two x values ( + 2x and – x). This leaves us with +3 standing alone and all the other numbers grouped separately. After grouping them together, you will get a simplified version of the expression as such:
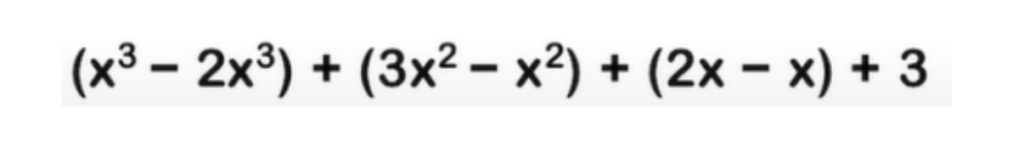
From here on, it is a matter of applying normal mathematical subtraction or addition, wherever required. (x^3 – 2x^3 = -x^3), (3x^2 – x^2 = 2x^2), (2x – x = x) and +3 remains as it is. The final simplified algebraic expression will therefore look like this:
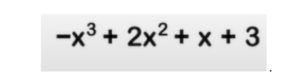
The above example was one where the positive/plus sign ( + ) was in front of all the brackets. At the exam, if you get a question where you get the negative/ minus sign ( – ) instead, apply this to all the terms inside the brackets.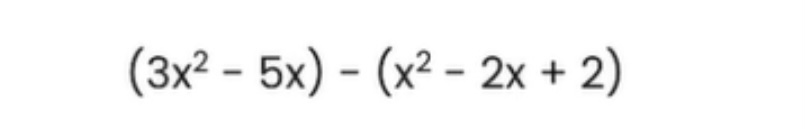
In the above example, there is a minus sign in front of the 2nd bracket. Therefore, once this sign is applied to all the terms inside the bracket, the terms will become (- x^2 + 2x – 2). The original – 2x becomes + 2x because a minus value and another minus value make a positive value.
The next few steps are quite similar to those in the first example:
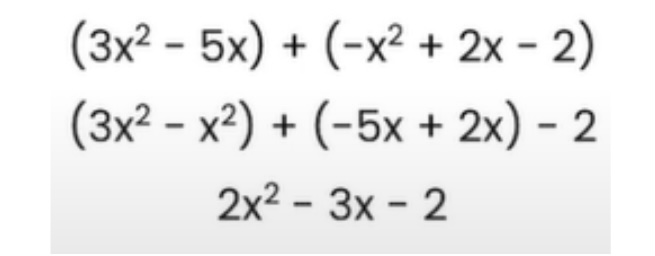
Expanding Brackets
Expanding brackets is also called the distributive law.
When expanding brackets, we are multiplying the term that is on the outside of the bracket, with every term that is on the inside of the bracket. You must never forget to take the signs ( + or – ) in front of these numbers).

In this example, 2x is multiplied with 3x, with + y and with -4z separately.
2x ✖ 3x = 6x^2
This is because exponent law will say that the powers will add up as x^1 ✖ x^1 .
(If you need to brush up on your knowledge of exponents and surds, we’ve got just the right article for you!)
Then we have (2x ✖ y), which then becomes 2xy and (2x ✖ – 4z) which becomes – 8xz because of multiplication.
Another example is when you get an expression like this:
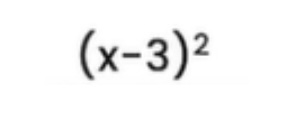
This is an important example. Whenthere is an expression as the one given above, this means that the term (x – 3) is repeated twice, essentially one (x – 3) is multiplied with another (x – 3).
Remember, you can’t just simplify by squaring the first term and by squaring the last term. When this happens, there is a term in the centre that will be missed and your entire answer will go wrong from that point on.
Therefore, to ensure that you don’t miss the centre term, you have to remember that whenever any bracket is squared, it has to be written as this bracket multiplied by itself, and then you have to go about planning an expansion step by step.
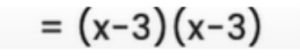
And in this expansion what you can see is, x in the first bracket has to multiply the x in the second bracket, and – 3 in the second bracket. Likewise, -3 in the first bracket has to multiply x in the second bracket and – 3 in the second bracket as well.
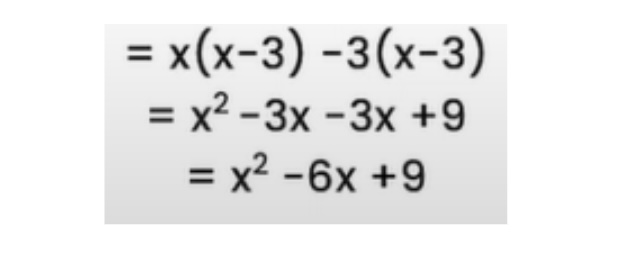
Dividing Expressions
When dividing expressions, we must try and figure out if there are factors that are common. 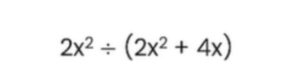
In the example above, we can see that in the denominator (2x^2 + 4x), common factors of 2 and x can be pulled out.
Once 2x is taken out, this becomes 2x (x + 2). With this, the 2 in the numerator and denominator can be removed.
That leaves x^2 as the numerator, and this will cancel the x in the denominator.
The final answer can be arrived at using this method: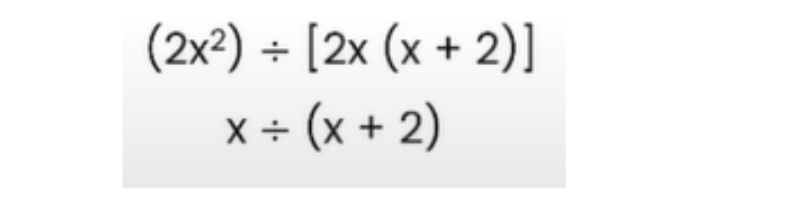
We are going to look at indices. 5^2 is 25. 5^2 is index form. 5 * 5 is expanded form and 25 is numerical form. These are notations and words you should be aware of.
Make Simplifying Algebraic Expressions Simple!
Simplifying Algebraic Expressions is closely related to the lessons Factorisation and Indices. To revise these two areas, you can watch the videos here and read the articles on factors and indices as well.
Algebra is an area that students tend to give up on because it looks hard and complicated. Inreality, it is one of the simplest concepts to learn. Once you practise enough questions, you will become comfortable with seeing long expressions on paper. Some questions can be found here as well, and you can time your answers to see if you can stick to the time limit given.
If you are struggling with IGCSE revision or the Mathematics subject in particular, you can reach out to us at Tutopiya to join revision sessions or find yourself the right tutor for you.
Watch the video below for a visual explanation of the lesson on simplifying algebraic expressions and make sure to attempt the quiz once you’re done!
