[Please watch the video attached at the end of this blog for a visual explanation of standard form]
In today’s article, we will be discussing the basics of standard form, an often-tested area that tends to confuse a lot of students.
What is Standard Form?
Standard form is a method of writing numbers by following a set of rules that are given to us.
If a number is
- Between 1.0 and 10.0
- Written as a decimal number
- Is multiplied by a power of 10
Then this number is said to be in standard form.
A simple reason behind using the standard form is to write huge numbers and very small numbers in a much more convenient format. Rather than seeing many zeroes on a page, your work becomes infinitely neater once the standard form is used, which is an additional bonus! ?
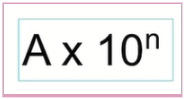
If you look at the picture above, you can see that there are two components. A represents any number between 1 and 10, and we also have 10n (read as 10 to the power of n), where n can also represent any integer, both positive and negative.
Ex: 3.2 ✖ 106 is a number that is written in standard form. This is because 3.2 is between 1 and 10, and then we also have 10 to the power of a number (106).
If this sounds confusing, you do not have to worry one bit as the examples below will illustrate how to convert numbers to standard form.
- Just know that the value of A has to be between 1 and 10. That is one of the most important things about standard form.
Converting numbers in standard form to their ordinary form
The ordinary form in this instance is the number where we have hundreds and thousands.
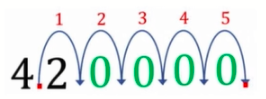
Ex: Express 4.2 ✖ 105 in its ordinary form.
- We can first consider 105 (read as 10 to power 5). This number basically stands for 10 ✖ 10 ✖ 10 ✖ 10 ✖ 10, which will equal to 100,000.
- We can then multiply 4.2 by 100,000, and to do that, we move the decimal point 5 times to the right.
- The answer is 420,000
- To see how you can get this answer quite easily in the calculator, refer to the video below!
Converting large ordinary numbers into standard form
Ex: Write 56,700,000 in standard form
- You have to first find out where you will put the decimal point so that the number is between 1 and 10.
If the decimal point is after 7, then the number will be 567. , which is too big and not between 1 and 10.
We can put the decimal point after the 6, but then it will be 56.7 which is once again, too big.
Therefore, in order to be ideal, the decimal point has to be between 5 and 6. When we put it between 5 and 6, we can see that the value can be written as 5.67, and this value is between 1 and 10.
2. Then we must decide times 10 to the power of what number should be put in the place of n.
To do this, we must see how many jumps are needed in order for this number 5.67 to become the original number given to us. Simply put, we need to see how many times the decimal point should be moved. We can see that in order for 5.67 to become 56,700,000, then we need to move the decimal point 7 times to the right side, and therefore, n = 7.
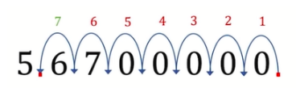
3. Hence, the way to write 56,700,000 in standard form is 5.67 ✖ 107.
Converting numbers in standard form to small ordinary numbers
Ex: Convert 8.9 ✖ 10-9 to standard form.
In the earlier example, when we had a positive value for n, we moved the decimal point to the right-hand side. However, when you have a negative power, you must move the decimal point to the left-hand side.
- Therefore, we have to move the decimal point in 8.9, nine times to the left-hand side
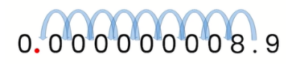
The final answer then becomes 0.0000000089
As seen in the above examples, it is quite easy to work with 8.9 ✖ 10-9 rather than work with a number with so many decimal points, and that is why standard form makes life so much easier!
Helpful points for practicing standard form for your upcoming Cambridge IGCSE Mathematics exams.
Mathematics is a subject that relies heavily on how well you prepare in advance for your exams. To make things easier, here are a few pointers that may help you get ready for your upcoming Cambridge IGCSE Mathematics exams.
Study the rules around standard form and make sure you apply them whenever you get a standard form question.
Practice sample questions – Standard form questions are quite common, especially in the short question paper, so practice all types of questions you can get your hands on before exams. Our question banks have questions of different difficulty levels that you can practice before your actual exams.
Practice past paper questions to familiarise yourself with the format of the questions and paper.
Ask for help – You are never too late to ask for assistance if you’re struggling. Reach out to us at Tutopiya to find the right tutor to help you pass your exams with flying colors!
Watch the video below for a visual explanation of standard form and attempt the quiz to challenge yourself!
